Conceptos básicos y organización de datos
Introducción
Debemos diferenciar dos tipos de estadística:
Estadística teórica que se ocupa de aspectos formales y educativos.
Estadística aplicada que constituye la aplicación a un campo concreto. Ha tenido distintos nombres, entre ellos “Análisis de Datos”.
La investigación en psicología
Utiliza el método científico, que se caracteriza por ser sistemático (sigue un sistema) y replicable.
Sus fases son:
Definición del problema.
Deducción de hipótesis contrastables.
Establecimiento de un procedimiento de recogida de datos.
Análisis de los resultados obtenidos (de este punto se ocupa la asignatura).
Discusión de dichos resultados y búsqueda de conclusiones.
Elaboración de un informe de investigación.
Concepto y funciones de la estadística descriptiva e inferencial
La estadística se ocupa de la sistematización, recogida, ordenación y representación de los datos referentes a un fenómeno que presenta variabilidad o incertidumbre para su estudio metódico, con objeto de hacer previsiones sobre los mismos, tomar decisiones u obtener conclusiones. Teniendo en cuenta las funciones podemos considerar dos grandes áreas:
Estadística descriptiva: se organizan y resumen conjuntos de observaciones procedentes de una muestra o de la población total, en forma cuantitativa. Los procedimientos para una variable: índices de tendencia general, estadísticos de variabilidad y estadísticos de asimetría; y para dos variables: coeficientes de correlación y ecuaciones de regresión.
Estadística inferencial: se realizan inferencias acerca de una población basándose en los datos obtenidos a partir de una muestra. Los procedimientos: el cálculo de probabilidades.
Conceptos importantes: población es el conjunto de todos los elementos que cumplen una determinada característica objeto de estudio. Muestra es un subconjunto de una población.
Parámetro es una propiedad descriptiva (medida) de una población. Estadístico es una propiedad descriptiva (medida) de una muestra.
Las conclusiones obtenidas de una muestra sólo servirán para el total de una población si la muestra es representativa. Para asegurarnos que la muestra es representativa se utilizan métodos de muestreo probabilístico.
También existes las muestras no probabilísticas como por ejemplo la muestra de conveniencia o incidental.
La medición y escalas de medida
Medición: Es el proceso por el cual se asignan números a objetos o características según determinadas reglas
Característica: Cualquier propiedad de objetos o personas que deseamos estudiar.
Modalidad: Distintas formas de presentarse esta característica. (Se le asina un número a cada una de las modalidades de una característica).
Escala Nominal: asignación de números o símbolos. Por lo tanto la única relación que obtenemos es la de igualdad o desigualdad. (Ej: católicos: (1) praticantes, (2) no praticantes).
Escala Ordinal: aparte de decirnos la igualdad o la diferenciación, también nos indica el orden de las posiciones de lo que está clasificado. Nos permite establecer relaciones del tipo “mayor que” o “menor que”. (Ej: Estatus socioconómico, bajo (1), medio (2), alto (3). Los números no solo indican diferencia de modalidades sino también orden entre ellas).
Escala de Intervalo: Además de las características de la escala nominal (igualdad o desigualdad) y de la escala ordinal (orden), la escala de intervalo se identifica porque cada número es una unidad de medición, podemos sumarlos o restarlos obteniendo resultados coherentes, a diferencia de la escala nominal. Es importante señalar que en la escala de intervalo el origen es arbitrario. (Ej: En el conocido test de inteligencia, la escala comienza en 0, pero este 0 es arbitrario ya que si alguien lo obtiene no significa que no tenga absolutamente nada de inteligencia. Esta arbitrariedad indica que aunque una persona obtenga un coeficiente de 80 y otra 160, no significa que la segunda persona sea el doble de inteligente que la primera).
Escala de Razón: Además de todas las características de las 3 escalas diferentes, supera a las demás en que se puede establecer un punto de origen verdadero de valor 0, a diferencia del 0 arbitrario de la escala de intervalo. Es lo que se conoce como valor absoluto. (Ej: el peso o la altura).
Variables: clasificación y notación
Variable: Representación numérica de una característica que presenta más de una modalidad (valor) de un conjunto determinado. Si una característica tiene una única modalidad se llama constante.
Tipos de variables:
Cualitativa (nominal): clasificadas en; Dicotómica: 2 categorías (por ej: sexo) y Politómica: más de dos categorías (por ej: nacionalidad).
Casicuantitativa (ordinal).
Cuantitativa (de intervalos, de razón): clasificadas en; Discreta: valores fijos (por ej: número de hijos, no pueden haber 1,5) y Continua: puede haber medidas intermedias entre los valores (por ej: el peso, 85,5kg).
Aparte de esta clasificación existen más clasificaciones:
Variable independiente: Cualquier suceso que sospechamos es la causa de otro
Variable dependiente: Medida utilizada para estudiar la variable independiente
Variable extraña: Aquellas que pueden influir sobre la variable dependiente pero no nos interesa estudiar sus efectos.
Para referirnos a un valor cualquiera de la variable X se utiliza el subindice i (Xi ), siendo n el número de elementos que componen la muestra: Xi siendo i = 1, 2, 3 … n
Distribución de frecuencias
Una distribución de frecuencias es una representación de la relación entre un conjunto de medidas exhaustivas y mutuamente influyentes y la frecuencia de cada una de ellas.
Funciones:
Ofrecer la información necesaria para realizar representaciones gráficas
Facilitar los datos para obtener los estadísticos muestrales
Conceptos:
Frecuencia absoluta (ni): Número de veces que se repite cada uno de los valores de una variable. La suma de todas las frecuencias absolutas representa el total de la muestra (n)
Proporción o frecuencia relativa (pi): Cociente entre la frecuencia absoluta de cada valor de la variable (ni) y el número total de observaciones (n). pi = ni /n
Porcentaje (Pi): Valor de la frecuencia relativa (pi) multiplicado por cien: Pi = pi x 100
Frecuencia absoluta acumulada (na): Número de veces que se repita cada modalidad o cualquiera de las modalidades inferiores.
Proporción acumulada o frecuencia relativa acumulada (pa): Cociente entre la frecuencia absoluta acumulada de cada clase y el total de observaciones. pa = na / n
Porcentaje acumulado (Pa): Valor de la frecuencia relativa acumulada multiplicado por cien. Pa= pax 100
Distribución de frecuencias:
Si la variable cuantitativa es reducida (número de hijos) no hay problema, la utilizamos tal cual. Pero si ocurre que puede ser muy amplia (edad) debemos recurrir a la agrupación en intervalos.
La Amplitud de los Intervalos representa al número de unidades que tenemos dentro de cada intervalo. (No es lo mismo tener una amplitud de intervalos de 10 en 10 (11-20) (21- 30) (31-40) que de 5 en 5 (15-19) (20-24) (25-29)).
Obviamente al establecer intervalos siempre se pierde información. Por lo tanto hay que buscar equilibrio entre la precisión que buscamos y lo cómodo que sea trabajar con esos datos (si no estableciésemos intervalos podríamos encontrarnos con tablas de 100 filas).
Aunque tengamos un intervalo de edad (25-35) (36-45) no significa que no pueda haber personas con 35,5 años. Por lo tanto los intervalos (25-35) y (36-45) reciben el nombre de limites informados o aparentes. (aparentan ser lo que no son) ya que en realidad los límites verdaderos son (25,5-35,5) y (35,5-45,5). El límite superior exacto del primer intervalo (35,5) coincide con el límite inferior exacto del siguiente (35,5)
Distribución de frecuencias con los datos agrupados en intervalos de la variable edad:
Cálculo de límites exactos: Límite exacto = Valor informado (el que nos han dado) +- 0,5 x I
I = Instrumento de medida. (en el caso de las edades I = 1)
Punto Medio se haya sumando los dos valores del intervalo y dividiendo el resultado entre 2. (Ej: Tomemos el intervalo (26-35) = 26 + 35 = 61/2 = 35,5)
Intervalo abierto: Son los intervalos finales que se utilizan para no tener frecuencia nula. (Ej de edad: 76 años o más)
Representaciones gráficas
El Sistema de Coordenadas más habitual esta formado por:
- Eje vertical (ordenada o eje Y), Eje horizontal (abscisa o eje X), Origen (punto donde se juntan ambos ejes).
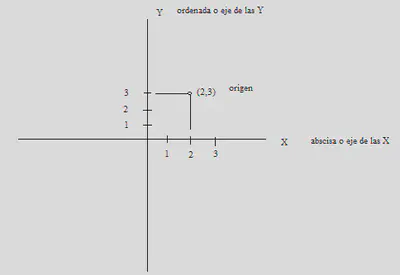
Representación gráfica de una variable
Diagrama de Barras
Se utiliza para variables nominales, ordinales y cuantitativas discretas.
En el eje X se colocan los valores y en el Y las frecuencias. Sobre cada valor de la variable se dibuja un rectángulo o barra perpendicular cuya altura debe ser igual a la frecuencia.
Diagrama de barras acumulativo: Variedad del diagrama de barras que se utiliza en variables ordinales y cuantitativas discretas. En el eje X se sitúan los valores de la variable y en el eje Y las frecuencias acumuladas.
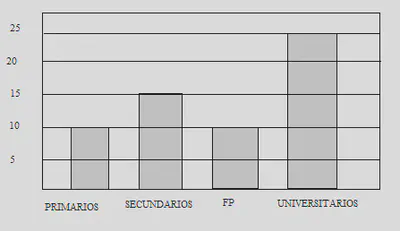
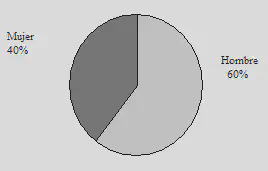
Diagrama de Sectores
Se utiliza para variables cualitativas y cuasicuantitativas
Representación en forma de círculo. El círculo se divide en secciones cuya superficie es proporcional a la frecuencia de la modalidad correspondiente. Para determinar el ángulo de los sectores de cada modalidad se multiplica la frecuencia relativa por 360, que es el número de grados de una circunferencia.
X ni pi Pi Grados Hombre 24 0,6 60 216 Mujer 16 0,4 40 144 n=40 1 100 360
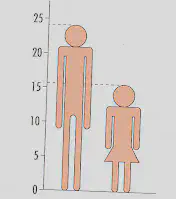
Pictograma
Se utiliza para variables cualitativas.
Son dibujos alusivos al objeto de estudio. Son escalas que deben ser proporcionales al valor que representan.
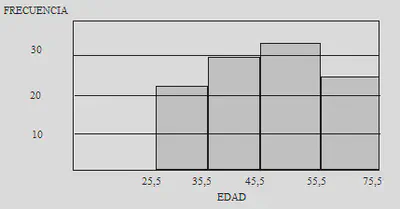
Histograma
Se utiliza para variables cuantitativas continuas con datos agrupados en intervalos
En el eje X se colocan los límites exactos de los intervalos y en el eje Y la frecuencia. (Parecido al diagrama de barras pero no hay espacio entre los rectángulos)
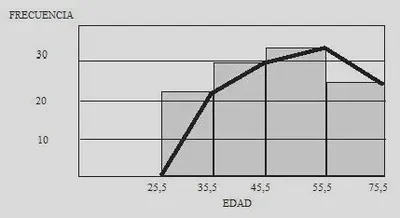
Polígono de Frecuencias
Se utiliza para variables discretas.
La forma que obtenemos es una línea poligonal cuya figura se obtiene a partir de una diagrama de barras o de un histograma.
También se puede utilizar en frecuencias acumuladas.
Representación gráfica de dos variables
Diagrama de barras conjunto
Se utiliza cuando al menos una de las dos variables es cualitativa
Los datos se organizan en una tabla de doble entrada. Se sitúan los valores de una variable en las filas y los valores de la otra variable en las columnas.
Una vez construida la tabla, se procede a dibujar los gráficos por columnas.
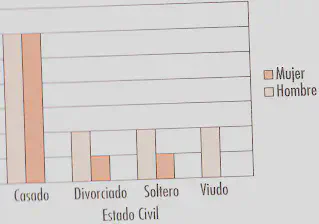
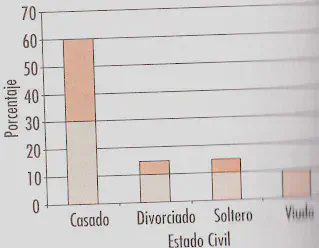
Diagrama de dispersión o Nube de Puntos
Se utiliza en el caso de dos variables cuantitativas
Una variable se sitúa en el eje X y la otra en el eje Y. Para cada par de datos se localiza la intersección entre ambas variables y se marca con un punto.
Es una manera rápida de hallar relaciones lineales entre las dos variables.

Propiedades de la distribución de frecuencias
Tendencia central
Se refiere al lugar donde se centra una distribución particular en la escala de valores.
Variabilidad
Se refiere al grado de concentración de las observaciones en torno al promedio.
Una distribución de frecuencias será:
Homogénea (tiene poca variabilidad). Si los valores de distribución están cercanos al promedio. (Cuando hay pocos rectángulos alrededor del central)
Heterogénea (tiene mucha variabilidad). Si los valores se dispersan mucho en torno al promedio. (cuando hay muchos rectángulos alrededor del central)
Asimetría o sesgo
Se refiere al grado en que los datos se reparten equilibradamente por encima y por debajo de la tendencia central.
Diremos que una distribución será simétrica cuando al dividirla en dos a la altura de la media, las dos mitades se superponen. Si esto no ocurre decimos que se produce asimetría. Hay dos tipos de asimetría:
Asimetría positiva: Cuando la mayor concentración de puntuaciones se produce en la parte baja de la escala.
Asimetría negativa: Cuando la mayor parte de puntuaciones se sitúa en la parte alta de la escala.