La investigación cuasi experimental
Introducción
La investigación cuasi experimental proviene del ámbito educativo, donde la investigación de ciertos fenómenos no podía llevarse a cabo siguiendo los procedimientos experimentales (Campbell y Stanley, 1966).
En las últimas décadas, han adquirido gran protagonismo en la investigación aplicada.
Características de los diseños cuasi experimentales
Se utilizan en situaciones en las que no se pueden asignar aleatoriamente los sujetos a las distintas condiciones.
Menor grado de control sobre los efectos de la VVEE que en los diseños experimentales.
Quien investiga puede…
Maximizar las diferencias en la VI (la varianza sistemática primaria).
Minimizar la varianza error.
Quien investiga no puede…
- Controlar la varianza sistemática secundaria causada por las amenazas a la validez interna.
El personal investigador no tiene recursos para controlar la formación de los grupos. La regla de asignación de los sujetos a los grupos no es aleatoria y, en la mayoría de los casos, no es conocida. Una de las principales tareas de quien investiga es identificar las posibles amenazas a la validez interna para tenerlas en cuenta o neutralizarlas. Tendrá que separar por otros medios los efectos debidos a la VI de los debidos a las VVEE que pueden influir en la VD (cuantos más factores extraños se descarten, mayor validez tendrá el estudio).
Mide los efectos del tratamiento sobre la VD (puede haber uno o más tratamientos).
Comparte la lógica del paradigma experimental que implica que, para poder establecer relaciones causales, se tienen que cumplir las siguientes condiciones:
La VI debe anteceder a la VD.
Debe existir covariación entre las variables.
Se deben poder descartar explicaciones alternativas. (Este es el punto que más problemas plantea en este contexto, pero es crucial para poder establecer inferencias causales)
La investigación se lleva a cabo en situaciones donde suele darse de forma natural la conducta objeto de estudio, por eso suele tener mayor validez externa (aunque, como hemos visto, si validez interna sea más débil)
Son de gran utilidad en la evaluación de programas de intervención psicológica o social, para mejorar su planificación y control.
Sirven para evaluar la efectividad y eficacia de los programas en diversos ámbitos: salud, educación, bienestar y otros servicios sociales…
Notación de los diseños cuasi experimentales
Introducida por Campbell y Stanley (1966) y posteriormente adoptada por Cook y Campbell (1979).

Diseño: O1 X O2 O3 ¬X O4
Grupos: 1
Medida pretratamiento: O1
Tratamiento: X
Medida postratamiento I: O2
Medida postratamiento II: O3
Retirada del tratamiento: ¬X
Medida postratamiento III: O4
Clasificación de los diseños cuasi experimentales
Según Campbell y Stanley, (1966) pueden ser:
Diseños pre-experimentales:
De un solo grupo, sólo con medida postest.
Sólo con medida postest, con grupo de control no equivalente.
De un solo grupo con medidas pretest+postest..
Diseños cuasi experimentales…
Con grupo de control:
Con grupo de control no equivalente…
Pretest+postest.
Cohortes.
Discontinuidad en la regresión.
Sin grupo de control:
Tratamiento repetido.
Retirada de tratamiento con pretest+postest.
De series temporales interrumpidas:
Simple.
Con grupo de control con equivalente.
Diseños pre-experimentales
(Cook y Campbell, 1979)
Sirven para aproximarse al fenómeno que se investiga (para generar hipótesis), sin olvidar que, en la interpretación de los datos, pueden existir numerosas VVEE que llevarían a una atribución errónea del efecto de la VI sobre la VD.
No suelen permitir establecer inferencias causales razonables.
Representan los módulos básicos a partir de los que se configuran el resto de los diseños cuasi experimentales.
Diseños de un solo grupo, sólo con medida postest: X O
- Carece de control, por lo que no se pueden extraer inferencias causales.
Diseños sólo con medida postest, con grupo de control no equivalente:
Sin pretest, no podemos saber si las diferencias entre los grupos (postest) se deben al tratamiento o a la selección diferencial (grupos no equivalentes).
Los resultados obtenidos no son interpretables en términos de causalidad.
Diseños de un solo grupo con medidas pretest+postest: O1 X O2
No podemos asegurar que los cambios (postest) se deban al efecto del tratamiento.
Existen numerosas amenazas a la validez interna: historia, regresión estadística, maduración, administración de test, instrumentación… Cuantas más descartemos, más podremos considerar que el diseño es interpretable (muy difícil).
Útil para sugerir hipótesis de cara a futuras investigaciones. (Más “rigurosas”)
Diseños cuasi experimentales con grupo de control
Diseños de grupo de control no equivalente
La regla de asignación a los grupos no es conocida porque se trabaja con grupos ya formados.
Aunque se trabaja con grupos ya formados, quien investiga tratará de seleccionar grupos lo más equivalentes posible, intentando que no influyan VVEE que pongan en peligro una interpretación unívoca de los resultados.
La lógica dice que si el tratamiento a tenido efecto, las diferencias entre los grupos (postest) serán mayores que las que pudieran existir inicialmente entre ellos (pretest).
Diseño pretest-postest con grupo de control no equivalente
Uno de los más utilizados en Ciencias Sociales.
Similar al diseño experimental de dos grupos aunque, aquí, los grupos ya están formados (no poseen la equivalencia inicial que se obtiene al asignar aleatoriamente los sujetos a los grupos). La medida pretest nos indicará las diferencias existentes antes de introducir el tratamiento.
La asignación del tratamiento a uno u otro grupo es controlada por el personal investigador.
Podemos encontrar diversos patrones de resultados sobre los que hay que analizar las amenazas a la validez interna.
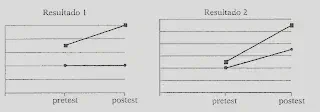
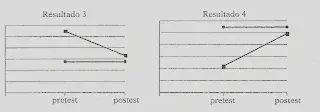

Instrumentación: Posible en los resultados 1 a 4. Difícil en el 5.
Regresión estadística: Posible en los resultados 1 a 4. Difícil en el 5.
Interacción selección x maduración: Posible en los resultados 1 y 2. Difícil en los resultados 3 a 5.
Interacción selección x historia (historia local): Posible en los resultados 1 a 5.
El resultado 5 es el más susceptible de interpretación en términos causales porque muestra un cambio de tendencia, de forma que el grupo que recibe el tratamiento tiene puntuaciones más bajas en el pretest que el grupo de control y más altas en el postest.
El análisis de datos se realiza con control estadístico podemos determinar la influencia de la VE sobre la VD. ANCOVA
El diseño de cohortes
El cohorte es el grupo de personas que pertenecen a algún tipo de institución (formal o informal) sometidos, durante un período de tiempo, a las mismas circunstancias. Van cambiando de un nivel a otro en dichas instituciones.
Muy útil en investigaciones del ámbito educativo. Ej: Primera promoción de estudiantes que vive una reforma educativa.
Tiene las siguientes ventajas:
Poder estudiar cómo un determinado acontecimiento afecta a un grupo (cohorte experimental) y compararlo con otro que no vivió dicho acontecimiento (cohorte de control).
Grupos fácilmente comprables, aunque no se llegue a la equivalencia conseguida con la aleatorización (no se puede descartar definitivamente la amenaza de selección). Permite establecer inferencias causales razonables (siempre evaluando si existen efectos de VVEE que interfieran en los resultados).
Como los grupos pertenecen a instituciones, el acceso a la información suele ser mejor porque existen numerosos archivos, registros…
Diseños de discontinuidad en la regresión
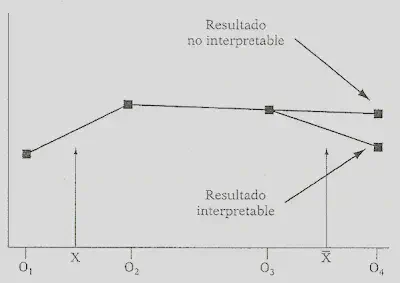
Este diseño tiene la ventaja de que permite establecer hipótesis causales con más garantías porque la regla de asignación a los grupos es conocida (alto grado de validez interna). Las personas van a un grupo u otro en función del pretest (C = Puntuación de corte a partir de la que unas personas se asignan al grupo de control y otras al grupo experimental).
Su nombre viene de calcular una recta de regresión a partir de las puntuaciones obtenidas (pretest+postest).
Fig. (a): Tratamiento sin efecto.
Fig. (b): Tratamiento con efecto (discontinuidad a partir del punto de corte “C”).
Como medida pretest, debe poder aplicarse una variable continua (en función de la que se formarán los grupos).
En la práctica, se utiliza poco porque la asignación a las condiciones no siempre se puede hacer de acuerdo a un único criterio. Suele utilizarse en…
Educación: Para valorar sistemas educativos.
Medicina: Para probar la efectividad de un medicamento.
Conocer la regla de asignación permite descartar algunas AMENAZAS a la validez interna, otras como la interacción entre tratamiento y maduración, no.
Diseños cuasi experimentales sin grupo de control
A veces no es posible disponer de un grupo de control (por razones prácticas y/o éticas). Tratamiento médico Tienen menos potencia para justificar inferencias causales que los diseños con grupo de control (menor validez interna). Algunos son más aconsejables como parte de diseños más complejos que como diseños independientes.
Diseño de retirada del tratamiento con pretest y postest
O1 X O2 O3 ¬X O4
Con la retirada del tratamiento, quien investiga, trata de crear unas condiciones que ejerzan la función del grupo de control. Ej: Secuencia experimental: O1 X O2 // Secuencia de control: O3 ¬X O4 (Vigilancia policial en barrio conflictivo).
Sólo puede aplicarse cuando el efecto inicial del tratamiento es transitorio.
El tratamiento es efectivo cuando las diferencias entre O1 y O2 están en dirección opuesta a las diferencias entre O3 y O4.
Posibles efectos del tratamiento entre O2 y O3 (aunque siga presente):
Incremento.
Mantenimiento.
Disminución.
Tras la retirada del tratamiento debe haber un cambio apreciable.
Presenta siguientes inconvenientes:
Se necesitan muestras grandes y medidas muy fiables.
A veces, la retirada del tratamiento puede plantear problemas éticos y/o frustración.
Puede producirse una alta mortalidad experimental.
Las observaciones deben hacerse a intervalos de tiempo iguales para controlar posibles cambios lineales espontáneos que tengan lugar dentro de un período de tiempo dado.
Diseño de tratamiento repetido
O1 X O2 ¬X O3 X O4
Se dispone de un único grupo en el que el personal investigador introduce, retira y vuelve a introducir el tratamiento, en diferentes momentos. La aplicación del tratamiento tiene que correlacionar con cambios en la VD.
Sólo puede aplicarse cuando el efecto inicial del tratamiento es transitorio.
Resultados más interpretables:
O1 difiere de O2.
O3 difiere de O4.
O3 - O4 difieren en la misma dirección que O1 - O2.
Presenta las siguientes amenazas:
Maduración cíclica (diferencias por el momento de registro y no por el efecto del tratamiento): Posible.
Historia: Poco probable. Sería mucha casualidad que un suceso externo produjera el mismo cambio que la introducción, retirada y reintroducción del tratamiento.
Diseños de series temporales interrumpidas
Toman varias medidas de la VD, antes y durante el tratamiento. Se realizan registros periódicos.
Para su análisis hay que saber en qué momento se introduce el tratamiento. Si es efectivo, las observaciones posteriores mostrarán un cambio en la serie.
Son frecuentes en:
Estudios sociales.
Estudios educativos.
Estudios sanitarios.
Evaluación de programas.
Diseño simple de serie temporales interrumpidas
O1 O2 O3 O4 O5 X O6 O7 O8 O9 O10 (Metadona)
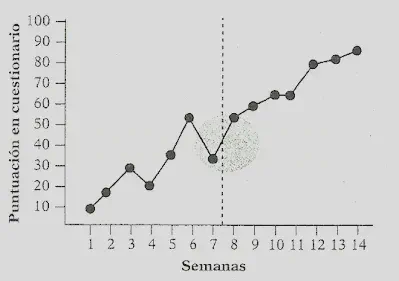
Requiere un solo grupo.
Es similar al diseño pretest-postest, pero se toman varias medidas antes y después de introducir el tratamiento.
El efecto del tratamiento se aprecia por la variación de la tendencia de la VD. Si el tratamiento es efectivo, dicha tendencia cambiará.
Posibles amenazas a la validez interna:
Maduración: Se puede controlar evaluando la tendencia pretratamiento (representando las observaciones anteriores al mismo).
Cambios cíclicos: El estudio de la serie temporal permite detectar y controlar su efecto (ventaja respecto a un diseño pretest-postest en el que podría darse de forma encubierta).
Regresión estadística: Puede controlarse estudiando la tendencia pre.
Instrumentación: Se puede controlar utilizando siempre el mismo procedimiento de registro.
Historia: Es la amenaza más difícil de controlar. Podría hacerse…
Acortando los intervalos temporales entre las medidas.
Aumentando el número de observaciones.
Midiendo simultáneamente las VVEE que pudieran influir en la VD, antes y después del tratamiento.
Evaluando el efecto de la retirada del tratamiento (sólo si éste es reversible).
Diseño de serie temporales interrumpidas con grupo de control no equivalente
Añadir un grupo de control es la mejor forma de controlar las amenazas a la validez interna.
Su punto fuerte y, a la vez, su principal dificultad es encontrar un grupo de control lo más semejante posible al experimental.